알고리즘과 선형알고리즘
파이만 알고리즘
1. 문제를 적는다.
2. 골똘히 생각한다.
3. 답을 적는다.
이 세상의 어떠한 어려운 문제도 해결할 수 있게 해 주는 우주 최강의 무적 알고리즘이라고 설명하고 있다.

일단 보면 너무 황당하다. 대부분의 사람들이 파인만같은 천재들만 사용할 수 있는 방법이라고 생각한다.
그런데, 사실 이 말은 같은 물리학자인 머리겔만? 이 말한 것으로 알려져있다.
결론부터 말하면 머리겔만이라는 사람이 파인만한태 열등감을 가지고 있어서 비꼬는식의 농담같은 거였다고 한다.
사실 이 이야기를 겔만이 했다는 뒷배경만 제외하고 나면 너무나 당연한 말이다.
모든 문제는 문제로서 인식하고, 깊이 생각하는 과정을 거쳐야 해결할 수 있다는 말이기 때문이다.
본론으로 들어가면
소프트웨어
소프트웨어를 설명할 때는 음식을 만드는 레시피에 자주 비유되곤 합니다.

위 예시 처럼요.
하지만 실제 프로그램에 필요한 내용을 알기에는 감이 잡히질 않는다. ( 그래서 뭘 어쩌자는 건가.. )
예를 들어, 초콜릿 케이크 레시피는
1. 오븐에서 30분, 또는 반죽이 자리 잡을 때까지 구우세요.
2. 표면 위에 손바닥을 살짝 올려서 확인하세요.
그런데 컴퓨터는 뭘 확인하라는건지, 반죽이 자리 잡을 때는 언제인지 너무 모호하게 표현되어있어서 제대로 동작할 수 없습니다.
( 적절한 예시는 아니다. )
그래서 납세 신고서에 비유하는 것이 더 적절하다고 합니다.
세금 계산은 어떤 상황에서도 납부할 정확한 세액을 항상 산출해 내야 하기 때문에 처리 절차가 완전해야 한다.
알고리즘
알고리즘은 세심하고 정확하게 작성된 레시피나 납세 신고서의 컴퓨터과학 버전이라고 할 수 있다.
결과를 정확하게 계산하도록 보장된 일련의 단계인셈이다.
알고리즘은 이루고 있는 모든 구성 요소의 의미에 한치의 모호함도 있어선 안된다.
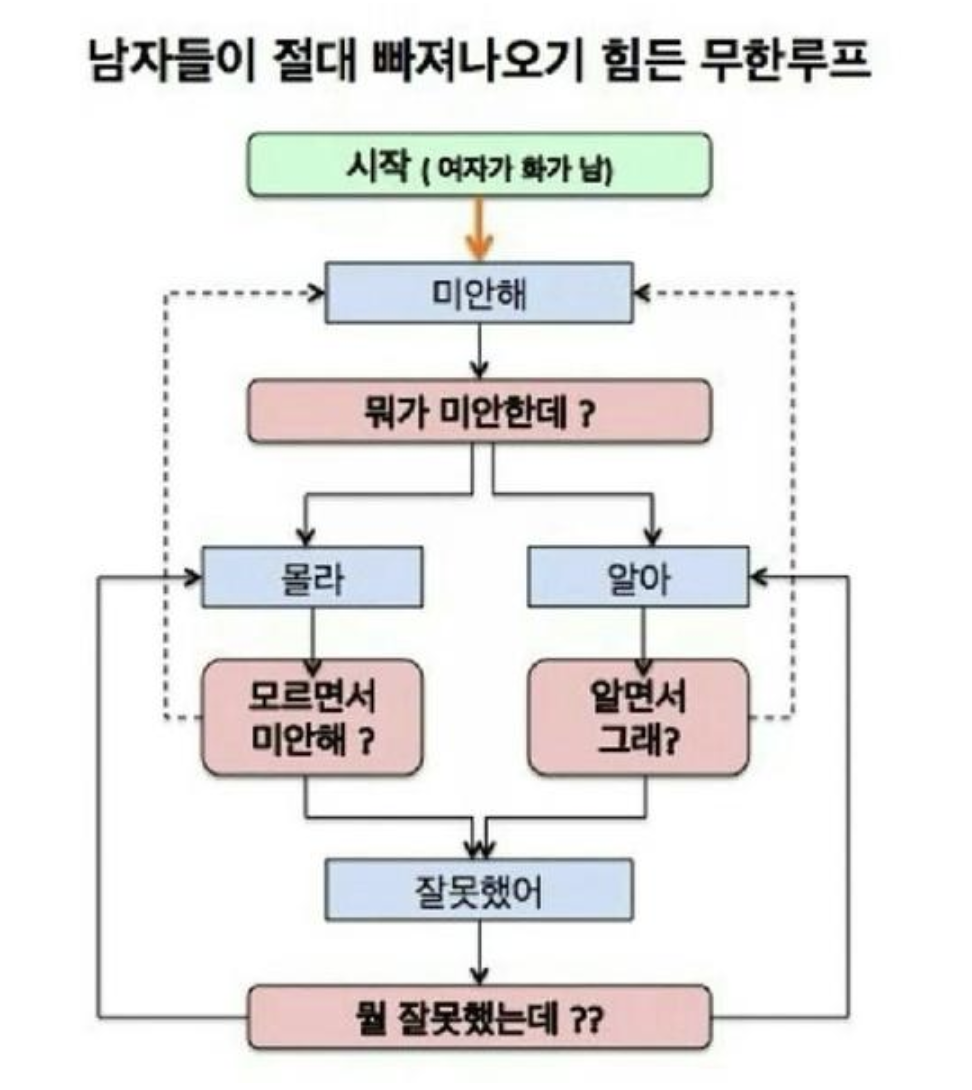
예를들어, 컴퓨터가 이런식으로 무한 루프에 빠지게 되면 이 알고리즘도 컴퓨터가 정확하게 처리하지 못하는 거죠.( 빠져나오려면 어떤 요구사항을 충족시켜 주어야 할까요? )
결론, 알고리즘은 지능이나 상상력이 없는 개체가 수행하더라도 연산의 의미와 수행 방법에 의심의 여지가 없을 정도로 상세하고 정확하게 일련의 연산을 명시해야 한다는 것이다.
선형 알고리즘
반에서 키큰 사람을 찾을 때 우리는 반 친구들을 줄 세우고 눈으로 쭉 확인하면 됩니다.
하지만 컴퓨터는 이 조차도 상세하게 알려주어야 하죠.
기본적인 접근 방식으로 한명한명 비교해가면서 가장 큰 친구를 찾는 방식이 있다.
그런데 만약 두 명 이상의 학생이 키가 같다면?
먼저 물어본 사람을 기록해야 할지, 나중에 물어본 사람을 기록해야 할지, 아니면 임의로 선택해야 할지... 정해야한다.
이런 문제를 해결하려면 자료 구조가 필요하다.
간단히 자료구조는 계산 과정에서 필요한 정보를 표한하는 방법이다.(자료구조도 열심히 배웠으니, 긴 설명은 패스)
흐음...그럼 각 반 친구들의 키의 평균을 계산하고 싶다면 어떻게해야 할까?
파이썬을 이용해서 표현해봤다.
height = []
sum = 0
for h in height:
sum += h
print(sum/len(height))
#ZeroDivisionError: division by zero사람이라면 이 작업을 하지 않아도 된다는걸 알 수 있다.
반 친구들이 없거나 키를 알 수가 없어서 평균을 구할 수가 없는 상황이다.
하지만 컴퓨터에게 이러한 상황에대한 가능성을 검사하게 해야하고, 그런 경우가 발생했을 때 어떻게 해야 하는지도 알려줘야 한다.
height = []
sum = 0
for h in height:
sum += h
try:
print(sum/len(height))
except ZeroDivisionError:
print('응~ 0으로는 못 나눠~')
알고리즘에서 중요한 특성 하나는 얼마나 효율적으로 작동하느냐다.
위에서 작성한 알고리즘은 반에 사람의 수 만큼 정비례하는 시간이 걸릴 것이다.
이러한 시간이 걸리는 알고리즘을 선형 시간 또는 선형 이라고 한다.
많은 선형 알고리즘은 동일한 기본 형태를 갖는다.
1. 먼저 초기화가 필요하다. (위에서 처럼 누적 합계를 0으로 설정하는것 처럼)
2. 그리고 값을 비교하거나 연산을 한다.
3. 마지막으로 끝내기 위한 단계가 필요하다. (합계를 나눠서 평균을 계산하는것 처럼)
